Hope everything is ok with you guys...
This week we had our midterm, I don't think I went bad in it, but there was a question in the test, if I'm not mistaken question 2, in which we had to negate a mathematical sentence, that for me was very confusing.
And it was not just negating, in that symbolic sentence we had to negate just the predicate.
Something like:
 x
x  X ,
X ,  y
y  X ,
X ,  z
z  X, x X y = z
X, x X y = z
And in the exercise we had to negate just the predicate. So:
x X y = z
And my problem was, how can I negate a multiplication? In the test I just thought, ok, so it must be the division.
Researching for this post, I remembered a thing, so basic. That the "and" operator is a way of representing multiplication, so basically:
x X y = z = ((x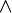 y)
y) 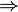 z)
z)
Translating the implication by its and/or form we arrive at:
(¬ (x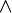 y)
y) 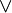 z)
z)
Negating this sentence by De Morgan's law we arrive at:
¬ ( (x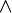 y)
y) 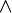 ¬ z )
¬ z )
I think that is the negation of the first sentence, I just thought that would be interesting to present something in this form to its derivation. Please, if my calculations, or logic are wrong, comment!
Something like:
 x
x  X ,
X ,  y
y  X ,
X ,  z
z  X, x X y = z
X, x X y = zAnd in the exercise we had to negate just the predicate. So:
x X y = z
And my problem was, how can I negate a multiplication? In the test I just thought, ok, so it must be the division.
Researching for this post, I remembered a thing, so basic. That the "and" operator is a way of representing multiplication, so basically:
x X y = z = ((x
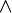 y)
y) 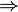 z)
z)Translating the implication by its and/or form we arrive at:
(¬ (x
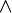 y)
y) 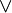 z)
z)Negating this sentence by De Morgan's law we arrive at:
¬ ( (x
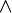 y)
y) 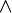 ¬ z )
¬ z )I think that is the negation of the first sentence, I just thought that would be interesting to present something in this form to its derivation. Please, if my calculations, or logic are wrong, comment!
 (
(